
The Hoeflin Power Test
Note: As of 4/12/03, the Hoeflin Power Test is no longer being scored by Ron Hoeflin
Published online with permission from the author:
Ronald K. Hoeflin
P.O. Box 539
New York, NY 10101
Send questions/comments related to this Web page to Darryl Miyaguchi
Change History:
| 04/12/03 | Ron no longer scores this test. |
| 09/24/01 | Fee increased from $20 to $30. |
| 04/05/01 | Fee decreased to $20. |
| 01/04/00 | Fee increased again from $25 to $33. |
| 12/20/99 | Removed any references in the body of this test to the Mega Test. |
| 4/22/98 | Fee reduced from $36 to $25. |
| 12/15/97 | Revised problems 23 and 24 to refer to a regular octahedron and dodecahedron. Change was approved by Dr. Hoeflin and suggested by Bruce W. McLain. |
| 6/24/97 | Corrected a typo in problem 31. Used to read: "Suppose someone who knows how the marbles were selected but now what their colors are ..." Thanks to Patrick Wahl for catching this. |
INTRODUCTION:
The Hoeflin Power Test, like the Raven Advanced Progressive Matrices and the ACT (akin to the SAT), measures intelligence or general aptitude on a 36-point scale. It is based on the best problems from my Mega, Titan, and Ultra tests, omitting verbal analogies and number sequences. The main objection to verbal analogies is that they are fairly culture-saturated, whereas the prevailing opinion is that a valid test of intelligence should downplay cultural mastery as much as possible. As for number sequences, some people do not even attempt them on the assumption that they require a significant background in mathematics. The advantage of a predominantly spatial test such as the present one is that it does give most people the feeling that they are exercising their intelligence when they try to solve the problems. These problems are not purely spatial but have significant verbal and numerical components inasmuch as one must understand the wording of the problems, which is occasionally rather intricate, and one must be able to perform various calculations, which is sometimes also a rather intricate task. In general, then, the test offers a fairly well-rounded intellectual exercise well suited to the assessment of general intelligence -- RKH.
INSTRUCTIONS:
1. ANSWER SHEET. Please print out the answer sheet (not yet available, but you can make your own) and write your answers there. Provide the other information requested too.
2. TIME LIMIT. There is no enforceable time limit, but it is suggested that you allot yourself an average of one day per problem, or a total of 36 days, which you can spread out over a several-months period, as for example if you only work on the test on weekends.
3. ADDITIONS AND CORRECTIONS TO ANSWERS: No additions or corrections to your initial set of answers will be accepted. You get only one try at this test, so do your best the first time.
4. ASSISTANCE. Use no calculating devices (except paper and pencil), and consult no books (except where indicated), or people (except RKH).
5. DISCUSSION OF PROBLEMS. As the Hoeflin Power Test may be used in the future as an admissions test to several societies, please do not share answers in a public forum with anyone who has not tried this test already. If you have plans to take Hoeflin's other tests (the Mega, Titan, or Ultra), then you should not share answers at all.
6. GUESSING. There is no penalty for wrong answers or guesses, so it is to your advantage to guess whenever you are unsure of an answer.
7. FEE. There
is $30 scoring fee, payable to the test
designer, "Ronald K. Hoeflin," at P.O. Box 539, New
York, NY 10101, U.S.A. Checks or money orders must be made
payable in U.S. dollars through any U.S. bank or post office.
Please remember that postal delivery services which require a
signature cannot be delivered to post office boxes. You will
receive a scoresheet showing your raw score. After a sufficient
number of people have taken the test (only 7 people had taken it
as of April 30, 1997), you will also receive your corresponding
I.Q. score, and its estimated percentile in the general
population.
8. SCORESHEETS. Send to Ronald K. Hoeflin at the above
address. Allow up to four weeks to elapse before complaining
about not receiving a score report. Most scores are sent out
within two or three weeks of the receipt of your answers.
9. SOCIETY ADMISSIONS USAGE: This test may be accepted in the future as an admissions test by high-IQ societies such as the Top One Percent Society, the One-in-a-Thousand Society, the Glia Society, the Triple Nine Society, the Prometheus Society, or the Mega Society.
10. PREVIOUS ATTEMPTS: If you tried any or all of my previous tests upon which this test is based, you can still try this test if you believe it would give a valid measure of your intellectual ability. -- RKH.
Overlapping Square Problems
| 1. | What is the minimum number of square sheets of paper sufficient to replicate the pattern to the right if the sheets of paper are unfolded, uncut, unmarked, and opaque and are placed flat on top of one another so that each line shown represents the edge of one of the squares insofar as it has not been occluded by an overlapping square? |  |
| 2. | As in the foregoing problem, find the minimum number of square sheets of paper sufficient to create the pattern shown to the right. |  |
Intersecting Surfaces
| 3. | Suppose that three intersecting rectangles are drawn on a flat surface. What is the maximum number of completely bounded areas, not further subdivided, that can thereby be formed, considering only the sides of the rectangles as boundaries? (The figure to the right illustrates two intersecting rectangles.) | 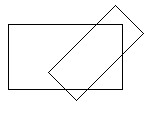 |
| 4. | Three mutually intersecting circles (as illustrated to the right) can yield a maximum of seven completely bounded areas, counting only areas that are not further subdivided. What is the maximum number of completely bounded areas not further subdivided that can be obtained using three mutually intersecting circles plus two triangles? | 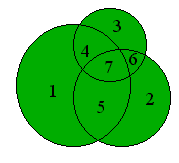 |
Lightbulb Problems
| 5. | If lightbulbs are placed at any two distinct vertices of a regular, i.e., perfectly symmetrical, dodecahedron, how many distinct patterns are possible, counting as one pattern any patterns that can be made to coincide with one another by merely rotating the dodecahedron in various ways as one solid object (See figure to the right.) | 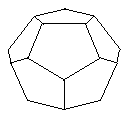 |
| 6. | Suppose that lightbulbs are placed at any three distinct vertices of a regular, i.e., perfectly symmetrical, icosahedron, as illustrated in the figure to the right. How many distinct patterns can thereby be formed, counting as one pattern any patterns that can be made to coincide with one another by merely rotating the icosahedron in various ways as one solid object? | 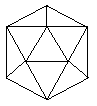 |
Painted Polyhedra
| 7. | If each side of a tetrahedron is an equilateral triangle painted white or black, five distinct color patterns are possible: all sides white, all black, just one side white and the rest black, just one side black and the rest white, and two sides white while the other two are black. If each side of an octahedron is an equilateral triangle painted white or black, how many distinct patterns are possible? |
| 8. | If each side of a cube is painted red or blue or yellow, how many distinct color patterns are possible? |
Drawing Problem
| 9. | Several identical cubes are fused together to form a solid object. Given the following five external views of such an object, draw the sixth external view. Clockwise or counterclockwise rotations of the sixth view are acceptable, but a mirror image (the sixth side as viewed from inside the solid) is not acceptable. |
|
Slicing Problems
| 10. | Suppose a perfectly spherical onion is sliced six times by perfectly straight (i.e., planar) knife strokes, the pieces thereby formed never moving from their initial positions. What is the maximum number of pieces into which the infinitesimally thin outer skin of the onion can thus be divided? (The figure to the right illustrates two knife strokes.) |  |
| 11. | Suppose a tetrahedral lump of clay is sliced by six perfectly straight (i.e., planar) knife strokes, the pieces thereby formed never moving from their initial positions. What is the maximum number of pieces -- tetrahedral in shape -- that can thereby be formed? | |
| 12. | Suppose a cube of butter is sliced by five perfectly straight (i.e., planar) knife strokes, the pieces thereby formed never moving from their initial positions. What is the maximum number of pieces that can thereby be formed? (The figure to the right illustrates three knife strokes.) | 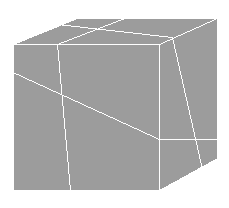 |
| 13. | Suppose that a doughnut (i.e., a torus-shaped solid object) is sliced three times by a knife, the intersection of the knife with the doughnut each time creating the shape of a Möbius strip. What is the maximum number of pieces into which the doughnut can thereby be sliced if the following definitions and restrictions are observed? A Möbius strip is a one-sided surface that is equivalent to the shape that would be formed by holding one end of a rectangle fixed, rotating the other end of the rectangle 180 degrees, and attaching it to the fixed end. A torus is created by rotating a circle about an axis in its plane that does not intersect the circle. The Möbius strips are to be regarded as perfectly elastic so that they form perfectly smooth surfaces free of any undulations or other distortions, and each making exactly one loop about the torus. The pieces formed never move from their initial positions in the torus. (The figure to the right illustrates a Möbius strip.) |  |
Weight Problems
| 14. | The figure illustrating this problem shows a scale for weighing objects, consisting of a lever resting on a fulcrum with weighing pans at each end of the lever equidistant from the fulcrum. Suppose that the objects to be weighed may range from 1 to 100 pounds at 1-pound intervals: 1, 2, 3, ..., 98, 99, 100. After placing one such weight on either of the two weighing pans, one or more precalibrated weights are then placed in either or both pans until a balance is achieved, thus determining the weight of the object. If the relative positions of the lever, fulcrum, and pans may not be changed, and if one may not add to the initial set of precalibrated weights, what is the minimum number of such weights that would be sufficient to bring into balance any of the 100 possible objects? | 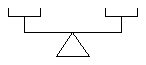 |
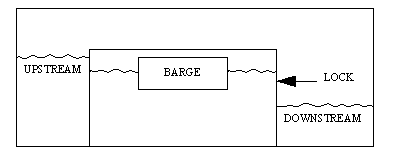
| 15. | A certain lock for raising and lowering barges from one river level to another is a rectangular parallelepiped 200 meters long, 50 wide, and 20 deep. A barge is floating in the lock that is also a rectangular parallelepiped measuring 80 meters long, 25 wide, and 5 deep. The barge, containing 3,000 barrels of toxic chemicals, displaces 8,000 long tons of water. The water has a density of one long ton per cubic meter. Each barrel is watertight, with a volume of one cubic meter and a weight of two long tons. A group of terrorists render the lock inoperable and attach a time bomb to the side of the barge set to go off in three hours. The barge contains elevators for moving barrels quickly to the deck, but the crew is too shorthanded to roll the heavy barrels up an inclined plane in the time allotted. The deck is only ten centimeters below the top edge of the lock, from which the barrels could be rolled to dry land. If no water is entering or leaving the lock, how many barrels at a minimum would have to be rolled into the water in the lock in order to raise the level of the barge so that its deck would be even with or slightly above the top edge of the lock so that the remaining barrels can be rolled to dry land? | |
Game Problems
| 16. | In going from square A to square B in the figure, what is the maximum number of squares that a chess knight could touch, including A and B, if the knight makes only permissible moves for a chess knight (consult a book on how to play chess if in doubt), does not touch any square more than once, and does not go outside the 16 squares shown? |  |
| 17. | Suppose a modified version of the dice game craps is played with two regular (i.e., perfectly symmetrical) dodecahedra. Each die has its sides numbered from 1 to 12 so that after each throw of the dice the sum of the numbers on the top two surfaces of the dice would range from 2 to 24. If a player gets the sum 13 or 23 on his first throw (a natural), he wins. If he gets 2, 3, or 24 on his first throw (craps), he loses. If he gets any other sum (his point), he must throw the dice again. On this or any subsequent throw the player loses if he gets the sum 13 and wins if he gets his point but must throw both dice again if any other sum occurs. The player continues until he either wins or loses. To the nearest percent, what is the probability at the start of any game that a dice thrower will win? | |


The Crystal Problem
| 18. | Suppose a tetrahedral-shaped crystal is formed, like a giant pile of apples or oranges at a greengrocer's store, consisting of one atom on the top layer, three on the next-to-top layer, six on the third layer, ten on the fourth layer, and so forth as illustrated below. If there are exactly 1,000,000 layers, specify the total number of atoms in the entire crystal. Give an exact answer, not an approximate one or a formula for making the calculation. | |

Cube Stack Problems
| 19. | Suppose 27 identical cubes are glued together to form a cubical stack, as illustrated to the right. If one of the small cubes is omitted, four distinct shapes are possible: one in which the omitted cube is at a corner of the stack, one in which it is in the middle of an edge of the stack, one in which it is in the middle of a side of the stack, and one in which it is at the core of the stack. If two of the small cubes are omitted rather than just one, how many distinct shapes are possible? |  |
| 20. | Suppose 27 identical cubical chunks of cheese are piled together to form a cubical stack, as illustrated to the right. What is the maximum number of these cheese chunks through which a mouse of negligible size could munch before exiting the stack, assuming that the mouse always travels along the grid of 27 straight lines that pass through the centers of the chunks parallel or perpendicular to their sides, always makes a 90 degree turn at the center of each chunk it enters, and never enters any chunk more than once? |  |
Crawling Ant Problems
Suppose there are ants at each vertex of a triangle and they all simultaneously crawl along a side of the triangle to the next vertex. The probability that no two ants will encounter one another is 2/8, since the only two cases in which no encounter occurs is when all the ants go left, i.e., clockwise -- LLL -- or all go right, i.e., counterclockwise -- RRR. In the six other cases -- RRL, RLR, RLL, LLR, LRL, and LRR -- an encounter occurs. Now suppose that, analogously, there is an ant at each vertex of a polyhedron and that the ants all simultaneously move along one edge of the polyhedron to the next vertex, each ant choosing its path randomly. For each of the following polyhedra, what is the probability that no two ants will encounter one another, either en route or at the next vertex? Express your answer reduced to lowest common denominators, e.g., 2/8 must be reduced to 1/4.
21. A tetrahedron
22. A cube.
23. A regular octahedron
24. A regular dodecahedron
Interpenetrating Solids
| 25. | If a cube and a tetrahedron interpenetrate one another, what is the maximum number of solid pieces (i.e., completely bounded volumes not further subdivided) that can thereby be formed? | |
| 26. | What is the maximum number of completely bounded volumes that can be formed by three interpenetrating cubes, considering only the surfaces of the cubes as boundaries and counting only volumes that are not further subdivided? | |
| 27. | Suppose two right circular cones and one right circular cylinder mutually interpenetrate, with the bases of each cone and both bases, i.e., both ends, of the cylinder sealed by precisely fitting flat circular surfaces. What is the maximum number of pieces, i.e., completely bounded volumes, that can thus be formed, considering only the surfaces of these three figures as boundaries and counting only pieces that are not further subdivided? If needed, consult a book for the definitions of "right circular cone" and "right circular cylinder." | |
Miscellaneous Problems
| 28. | Suppose five dots are arranged in a three-dimensional space so that no more than three at a time can have a flat surface pass through them. If each set of three dots has a flat surface pass through them and extend an infinite distance in every direction, what is the maximum number of distinct straight lines at which these planes can intersect one another? | |
| 29. | Suppose a diagonal line is drawn across each of the six sides of a cube from one corner to the other. How many distinct patterns are possible if one includes all six sides of the cube in each pattern and counts as one pattern any patterns that can be made to coincide by various rotations of the cube as one rigid object? | |
| 30. | Suppose the thirty edges of a regular, i.e., perfectly symmetrical, dodecahedron are rods, two of which are painted white and the rest black. How many distinct patterns can thus be created, counting as one pattern any patterns that can be made to coincide by various rotations of the dodecahedron as one rigid object? | |
| 31. | Suppose ten marbles are inserted into a box based on the tosses of an unbiased coin, a white marble being inserted when the coin turns up heads and a black one when the coin turns up tails. Suppose someone who knows how the marbles were selected but not what their colors are selects ten marbles from the box one at a time at random, returning each marble and mixing the marbles thoroughly before making another selection. If all ten examined marbles turn out to be white, what is the probability to the nearest percent that all ten marbles in the box are white? | |
Sequence Problems
For each of the following sequences of square patterns, determine the principle that underlies the organization of the sequence and draw the pattern that would appropriately fill in the square with the question mark in it.
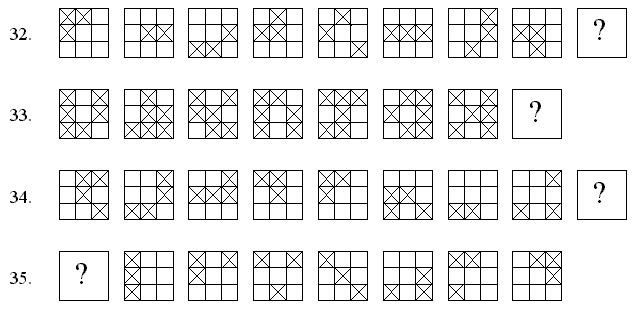
| 36. | 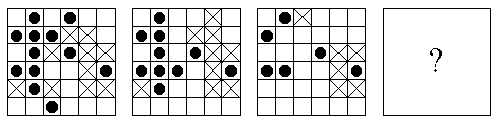 |
|
This concludes the test.
Return to the Uncommonly Difficult I.Q. Tests Page